Benchmarking de Storage: Da Teoria das Filas à Aprovação do CFO

Abandone métricas de vaidade. Aprenda a modelar a capacidade de armazenamento com rigor matemático, prever o ponto de saturação e justificar investimentos.
A lacuna entre a engenharia de sistemas e a diretoria financeira é, fundamentalmente, um problema de tradução. Enquanto o engenheiro observa latência de disco e profundidade de fila (queue depth), o CFO enxerga CapEx e risco operacional. Como Planejador de Capacidade, minha função não é apenas pedir mais discos; é modelar matematicamente o comportamento futuro do sistema para evitar o precipício de recursos.
O armazenamento (Storage) é o subsistema mais crítico e punitivo em termos de performance. Diferente da CPU, que degrada graciosamente (throttling), o storage atinge um ponto de saturação assintótico onde a latência cresce exponencialmente. Neste artigo, abandonaremos o misticismo dos datasheets de fabricantes e aplicaremos a física dos sistemas computacionais — inspirados na rigo-rosidade de Neil Gunther — para construir um caso irrefutável para a expansão de infraestrutura.
Consumo Atual: O Mito do 'Max IOPS' e a Realidade da Carga de Trabalho
O erro cardinal em qualquer planejamento de capacidade é confiar nos números de "Max IOPS" fornecidos pelo fabricante. Estes são, invariavelmente, "Hero Numbers": obtidos em condições de laboratório, com 100% de leituras (read), blocos de 4KB, acesso randômico perfeitamente alinhado e latência zero de rede.
O consumo atual real do seu ambiente é entrópico. Uma carga de trabalho de produção não é um fluxo constante; é um processo estocástico com rajadas (bursts) imprevisíveis. Para entender o consumo atual, precisamos decompor a métrica de IOPS em seus componentes vetoriais reais: Tempo de Serviço ($S$) e Tempo de Espera ($W$).
O IOPS observado é apenas a taxa de chegada ($\lambda$) que o sistema conseguiu processar. Se o seu sistema reporta 20.000 IOPS com uma latência de 50ms, você não está vendo performance; está vendo um sistema engasgado.
A Falácia da Média
Médias mentem. Uma média de latência de 5ms pode esconder picos de 500ms que causam timeouts na aplicação. O planejamento de capacidade deve focar nos percentis superiores (P95, P99). É aqui que a realidade da carga de trabalho se distancia dos testes sintéticos.
 Figura: Fig 2. A falácia do teste sintético vs. a entropia da produção real.
Figura: Fig 2. A falácia do teste sintético vs. a entropia da produção real.
Como ilustrado acima, a entropia da produção introduz variáveis que os benchmarks sintéticos lineares ignoram: lock contention no nível do banco de dados, garbage collection do array de flash e a "vizinhança barulhenta" em ambientes virtualizados. O consumo atual deve ser medido não pelo que o storage pode fazer, mas pelo headroom (margem de manobra) restante antes que a latência viole o SLA.
Taxa de Crescimento: Derivadas, Tamanho de Bloco e Padrões de Acesso
Projetar o futuro olhando apenas para o crescimento do volume de dados (Terabytes) é amadorismo. O espaço em disco cresce linearmente; a complexidade do I/O cresce geometricamente. Para um modelo preditivo robusto, precisamos analisar a taxa de crescimento da intensidade do I/O.
A Física do Throughput
O throughput (largura de banda) é o produto do IOPS pelo tamanho do bloco:
$$ Throughput = IOPS \times BlockSize $$
Muitos planejadores falham ao não perceber que uma mudança na aplicação (ex: alteração no tamanho da página do banco de dados de 8KB para 16KB) pode manter o mesmo número de IOPS, mas dobrar a exigência de throughput, saturando os controladores ou os links de Fibre Channel/iSCSI antes mesmo de saturar os discos.
Padrões de Acesso: Random vs. Sequential
A taxa de crescimento deve ser qualificada pelo padrão de acesso.
Acesso Sequencial: Geralmente limitado por largura de banda (MB/s). Comum em backups e logs.
Acesso Randômico: Limitado por IOPS e latência. Comum em OLTP (Online Transaction Processing).
Se sua taxa de crescimento de transações de banco de dados é de 10% ao mês, a degradação da performance não será de 10%. Devido à natureza mecânica (em HDDs) ou à amplificação de escrita e garbage collection (em SSDs/NVMe), um aumento linear na carga resulta em um aumento não-linear na latência quando nos aproximamos da capacidade máxima. Estamos lidando com derivadas: a taxa de mudança da latência em relação à taxa de mudança da carga.
O Ponto de Ruptura: Identificando o 'Joelho' da Curva de Latência
Aqui entramos no território da Teoria das Filas. O objetivo do benchmarking não é achar o limite máximo, mas encontrar o "Joelho" (The Knee) da curva. Este é o ponto onde o sistema deixa de ser limitado pela demanda e passa a ser limitado pela contenção de recursos.
A Lei de Little é a equação fundamental que rege este comportamento:
$$ L = \lambda W $$
Onde:
$L$ = Número médio de requisições no sistema (Queue Length).
$\lambda$ = Taxa de chegada (IOPS).
$W$ = Tempo médio de resposta (Latência).
Enquanto a utilização ($U$) do sistema for baixa, a latência ($W$) permanece constante e dominada pelo tempo de serviço do hardware. Contudo, conforme $U$ se aproxima de 1 (100% de utilização), o tempo de espera na fila explode matematicamente para o infinito.
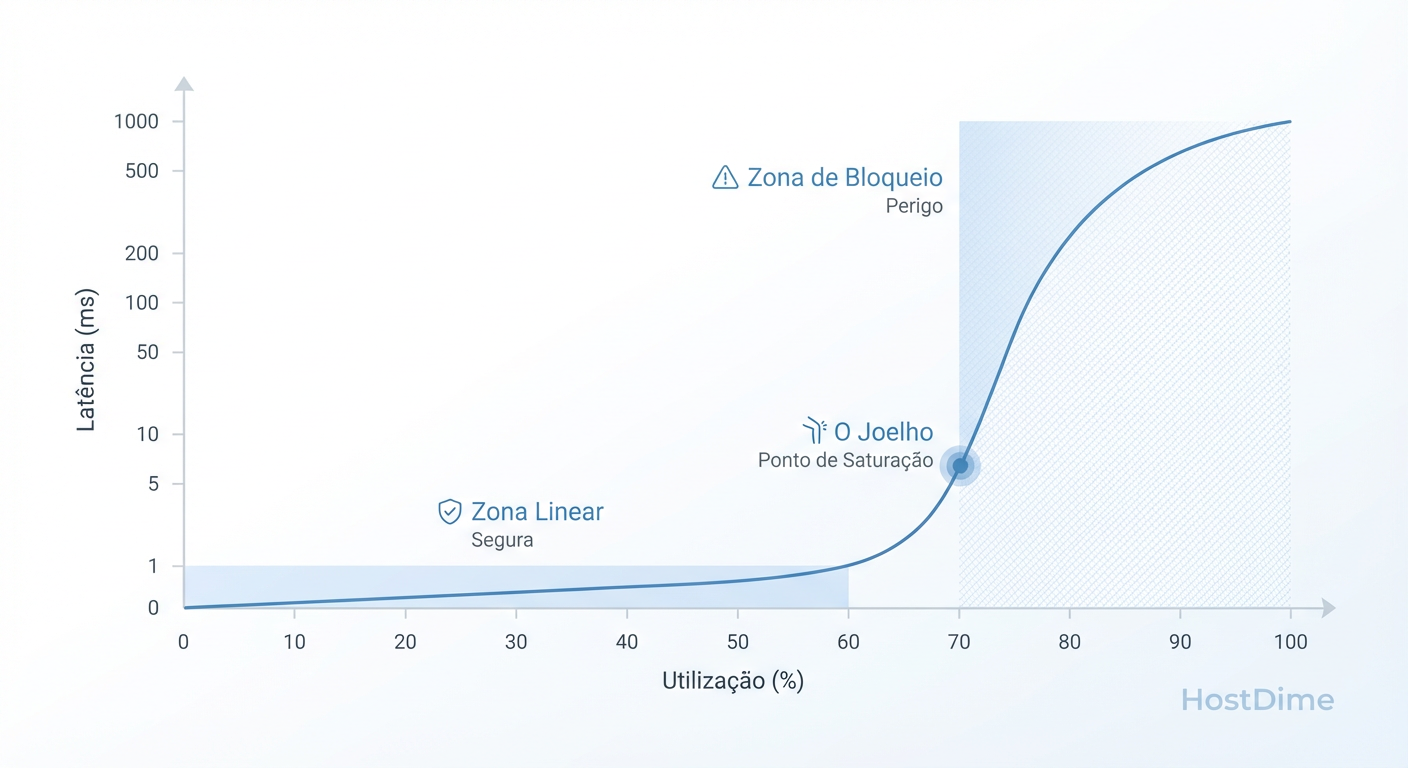 Figura: Fig 1. O 'Joelho' da Curva: Onde a Teoria das Filas dita o fim da performance aceitável.
Figura: Fig 1. O 'Joelho' da Curva: Onde a Teoria das Filas dita o fim da performance aceitável.
O "Joelho" da curva, visualizado acima, ocorre tipicamente entre 60% e 70% de utilização do controlador ou do meio físico. Operar além do joelho é suicídio operacional. A latência torna-se instável e pequenos aumentos na carga ($\lambda$) resultam em aumentos massivos no tempo de resposta ($W$).
O Perigo da Saturação Oculta
Em arrays All-Flash, a latência é tão baixa que o "joelho" é muito agudo. O sistema responde em sub-milissegundos até atingir a saturação, momento em que a performance cai verticalmente (o hockey stick effect). Identificar este ponto de ruptura via load testing é essencial para definir o limite de segurança do ambiente.
Estratégia de Expansão: Over-provisioning, Penalidade de RAID e Tiering Inteligente
Uma vez identificado o ponto de ruptura, a estratégia de expansão deve considerar as ineficiências inerentes à tecnologia de armazenamento. Não compramos "100TB de performance"; compramos capacidade bruta que é erodida por penalidades de escrita e overhead de proteção.
A Matemática da Penalidade de RAID
A escolha do nível de RAID afeta drasticamente o IOPS efetivo. Cada operação de escrita lógica (do ponto de vista do SO) gera múltiplas operações de I/O físicas no back-end (IOPS de Back-end).
| Nível de RAID | Penalidade de Escrita | Fórmula de Custo de IOPS | Uso Recomendado |
|---|---|---|---|
| RAID 0 | 1 | $1 \times Write$ | Cache efêmero (Sem proteção) |
| RAID 1/10 | 2 | $2 \times Write$ | OLTP de Alta Performance |
| RAID 5 | 4 | $4 \times Write$ | Leitura intensiva, Dados Gerais |
| RAID 6 | 6 | $6 \times Write$ | Arquivamento, Discos Grandes |
Se sua carga de trabalho é 50% escrita e você migra de RAID 10 para RAID 6 para "economizar espaço", você triplicou a carga nos discos para as mesmas operações de escrita. Isso desloca o "joelho" da curva para a esquerda, reduzindo a capacidade total do sistema.
Over-provisioning e Tiering
Em SSDs, o Over-provisioning (reservar espaço livre não formatado) é vital para manter a performance de escrita estável, permitindo que o controlador do SSD gerencie blocos inválidos sem travar o I/O.
A estratégia de Tiering Inteligente (mover dados frios para mídias lentas e dados quentes para flash) deve ser modelada com cuidado. Se o working set (dados ativos) crescer além da camada de Flash, ocorrerá o fenômeno de cache thrashing, onde o sistema gasta mais recursos movendo dados entre camadas do que servindo a aplicação.
Modelo de Previsão: Regressão Linear e a Lei Universal de Escalabilidade (USL)
Para convencer o CFO, precisamos de uma data. "Precisamos de storage ano que vem" é vago. "O storage atingirá o ponto de saturação de latência no dia 14 de novembro" é um argumento fiscal.
Modelos de regressão linear simples ($y = ax + b$) falham em sistemas de TI porque assumem escalabilidade infinita. Eles ignoram a contenda (recursos disputando acesso a dados compartilhados) e a coerência (o custo de manter os dados consistentes).
Aplicando a Lei Universal de Escalabilidade (USL)
Para uma previsão precisa, utilizamos o modelo de Neil Gunther, a USL, que define a capacidade relativa $C(N)$ em função da carga $N$:
$$ C(N) = \frac{N}{1 + \alpha(N-1) + \beta N(N-1)} $$
Onde:
$\alpha$ (alpha): O parâmetro de contenda (serialização).
$\beta$ (beta): O parâmetro de coerência (crosstalk).
Este modelo nos permite traçar a curva de degradação de performance muito antes dela acontecer. Podemos plotar os dados atuais de benchmarking e extrapolar onde a curva se achata (limite de throughput) ou regride (devido à coerência).
O Horizonte de Eventos Orçamentário
Ao cruzar a projeção da USL com a taxa de crescimento da carga de trabalho (derivada na seção 2), encontramos a data exata em que o sistema cruzará o limiar de latência aceitável (o SLA).
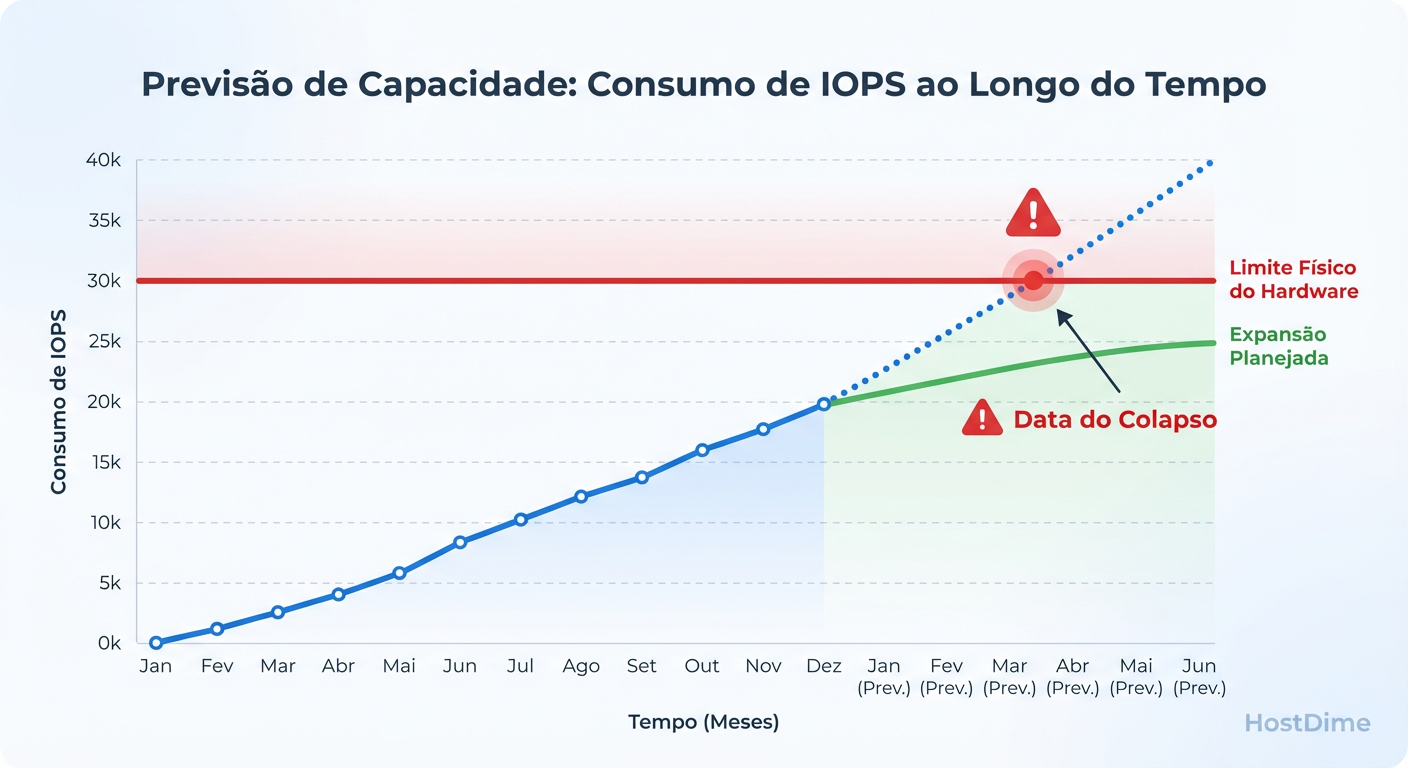 Figura: Fig 3. O Horizonte de Eventos: Projetando a data exata da saturação para justificar o budget.
Figura: Fig 3. O Horizonte de Eventos: Projetando a data exata da saturação para justificar o budget.
A Figura 3 representa o que chamo de Horizonte de Eventos. A linha vermelha vertical não é quando o disco enche; é quando a latência média projetada excede o requisito da aplicação crítica.
O Script de Projeção: Para engenheiros que desejam calcular isso, um snippet simples em Python utilizando regressão para estimar a tendência de crescimento de carga ($\lambda$) pode ser o ponto de partida para alimentar a equação da USL:
import numpy as np
from sklearn.linear_model import LinearRegression
# Dados históricos: [Mês, Carga_IOPS_P95]
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([12000, 12500, 13100, 13800, 14600])
model = LinearRegression()
model.fit(X, y)
# Previsão para o mês 12 (Budget Cycle)
future_month = np.array([[12]])
predicted_load = model.predict(future_month)
print(f"Carga Projetada para Mês 12: {predicted_load[0]:.0f} IOPS")
# Nota: Insira este valor na equação de Little para verificar a Latência esperada.
Veredito Técnico: A Linguagem do Dinheiro
A aprovação do CFO não vem de explicar o que é RAID ou latência. Vem da demonstração de que o custo da inação (risco de downtime ou lentidão sistêmica) supera o custo do investimento. Ao apresentar um modelo baseado na Teoria das Filas e na USL, você transforma uma "compra técnica" em uma estratégia de mitigação de risco financeiro baseada em dados irrefutáveis. O storage não é um balde; é um banco, e nós não podemos permitir uma corrida aos saques.
Referências
Gunther, Neil J. Guerrilla Capacity Planning: A Tactical Approach to Planning for Highly Scalable Applications and Services. Springer, 2007.
Little, J. D. C. "A Proof for the Queuing Formula: L = λW". Operations Research, 1961.
Jain, Raj. The Art of Computer Systems Performance Analysis. Wiley, 1991.
SNIA (Storage Networking Industry Association). Performance Test Specification (PTS) Enterprise.

Roberto Sato
Planejador de Capacidade
"Traduzo métricas de consumo em modelos de crescimento sustentável. Minha missão é antecipar gargalos e garantir que sua infraestrutura escale matematicamente antes de atingir o limite crítico."